Atmospheric Path Delay Correction Based on
the Numerical Prediction Data
ICHIKAWA, Ryuichi
Kashima Space Research Center
Communications Research Laboratory
893-1 Hirai, Kashima, Ibaraki 314, Japan
1. Introduction
Atmospheric path delay is a serious error source in measurements by very
long baseline interferometry (VLBI) both through ray path bending and the
modification of the electromagnetic wave velocity. The delay has been
separately discussed because of its causes; one is the "wet delay" due to
the dipole component of water vapor and the other is the "hydrostatic
delay" due to the nondipole components of atmospheric constituents.
Geodesists have especially focused their attention on devising techniques
for estimating the wet delay because of the significant variability of
water vapor. Conventionally, the wet delay for each site has been estimated
from a "zenith delay" and a "mapping function", with the latter function
describing the elevation angle behavior of the atmospheric path delay (e.g.
Chao, 1972; Davis et al., 1985).
The zenith wet delay is estimated from (1) a model relating surface
meteorological conditions to this delay (e.g. Saastamoinen, 1972), (2)
observation by using a ground-based water vapor radiometer (WVR) (e.g. Hogg
et al., 1983), and (3) parametric estimation by using a stochastic process
such as the Kalman filtering techniques (e.g. Herring et al., 1990; Tralli
et al., 1992). The mapping functions are constructed for a spherically
symmetric atmosphere. On the contrary, the atmospheric water vapor,
temperature, and pressure vary in various temporal scales and spatial
dimensions. Consequently, we exactly require an effective method to correct
the azimuthal asymmetry of the wet delay to attain sub-millimeter
accuracy.
2.Atmospheric Path Delay Estimated by Numerical Prediction Data
Recently, the numerical weather prediction model has been successfully used for
the purpose of the operational weather prediction. The three-dimensional
grid point data set is produced from the numerical weather prediction model
can be applied to estimate the wet delay.
Figure 1 shows a schematic figure of the global analysis (GANL) data set by
the Japan Meteorological Agency (JMA) (JMA, 1993). The GANL data are given
four times a day to a 1.875-degree latitude-longitude grid system with 16
layers (surface and 15 standard pressure levels, i.e., 1000, 850, 700, 500,
400, 300, 250, 200, 150, 100, 70, 50, 30, 20, and 10 hPa). At each grid
point meteorological elements, geopotential height, temperature, dewpoint
depression, and wind vector are computed from the data obtained by
radiosonde, aircraft, maritime and satellite observations, using a
multi-variate optimum interpolation method (Lorenc, 1981) together with the
forecast values.
Figure 2 shows the temporal variations of the zenith wet delay based on the
GANL data set and that from radiosonde observation at Tateno near Tsukuba
and Hachijojima in the West Pacific during the period from April 1988 to
February 1989. At both sites the zenith wet delay computed from radiosonde
data varies from 5 to 20 cm in winter (January), and from 20 to 40 cm in
summer (July). Moreover, the amplitude of delay variation within the period
of several days reaches more than 10 cm during all seasons. The zenith wet
delay based on the GANL data set is well consistent with that from
radiosonde observations in both amplitude and phase through the period. It
is clear that the GANL data set exhibits a good recovery of the observed
meteorological conditions.
JMA developed finer mesh model, named the 10 km spectral model to forecast
mesoscale phenomena accurately as shown in Figure 3. The 10 km data are given
on a 97 X 97 latitude-longitude grid system with 10 km intervals (at 60
degrees N) and 12 layers (surface and 11 significant pressure levels, i.e.,
1000, 900, 850, 700, 500, 400, 300, 250, 200, 150, and 100 hPa) for the
purpose of the numerical prediction of mesoscale phenomena of the order
of 20-200 km, such as squall lines, cloud clusters and so on.
The outputs
from the model can be available to correct
the azimuthal asymmetry of the
wet delay.
Figure 4 shows an example of positioning errors due to the azimuthal
asymmetry of the wet delay numerically estimated by 10 km spectral model
(Ichikawa et
al., 1994). Minimum elevation angle of 15 degrees is assumed. According to
the figure, uncertainties of baseline vectors are up to several centimeters
in horizontal and more than one centimeter in vertical.
Figure 1. Grid system of the JMA (Japan Meteorological Agency) global
analysis data. (after JMA(1995)).
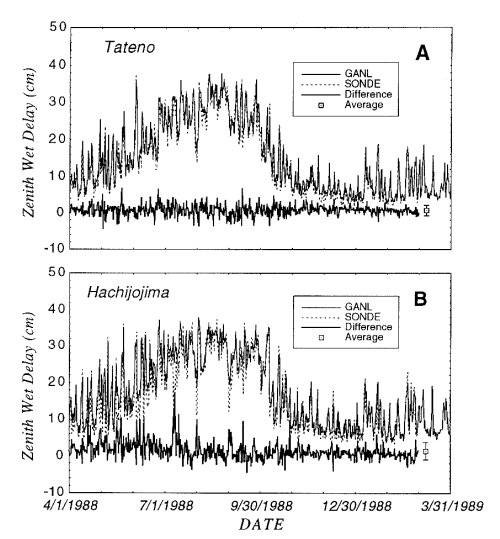
Figure 2. Daily variation of the zenith wet delay based on the global
analysis data set (solid line) and that from radiosonde observation (broken
line) during the period from April 1988 to February 1989 at Tateno (upper)
and Hachijojima (lower).
Figure 3. Forecast area of the JMA 10 km spectral model.
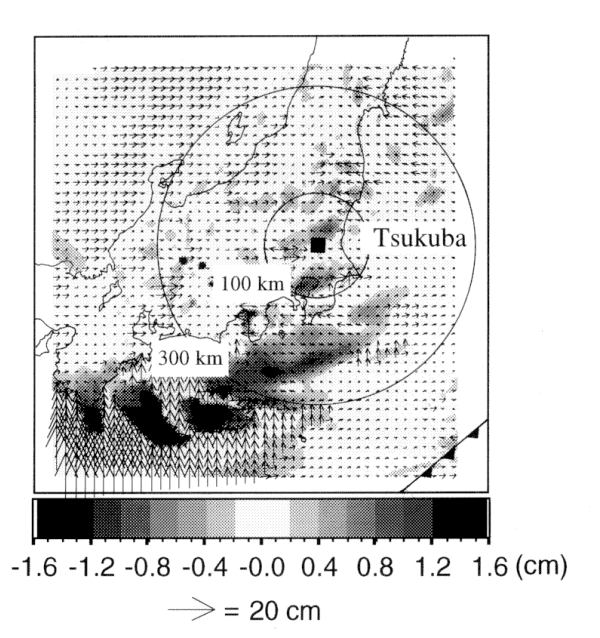
Figure 4. Estimated horizontal vectors and vertical components of the
apparent displacement vectors caused by the wet delay error due to the
azimuthal asymmetry of atmosphere. These apparent displacement vectors are
considered to be the relative positioning errors in measurements by VLBI.
Minimum elevation angles of radio sources are assumed to be 5 degrees.
Frontal position is obtained from JMA operational surface analysis.
3.Proposal of New Correction Method
The estimations of the wet delay by the numerical prediction data can be
easily applied to the correction of VLBI measurements considering the
azimuthal asymmetry. In the field of numerical weather prediction,
there has been much effort recently in developing more accurate models.
These new models are devised to take account of modeling the real
atmospheric motion and new meteorological observations such as satellite
microwave radiometry. These model data sets always keep the
three-dimensional scheme. Therefore, once an estimation system of the wet
delay is established, we can easily obtain more accurate estimates of
the delay when the numerical prediction model data set is up to date.
This new correction method has two advantages. First, the equally-weighted
correction to the delay is available wherever the VLBI measurements are
conducted. Second, re-examination and re-correction of the delay for the
past geodetic observations are always available by using the updated model
data in the future. It is expected that this will become a powerful
correction method. At present, I plan feasibility studies to evaluate the
availability of the numerical prediction data for correcting VLBI
measurements.
References
Chao, C. C. (1972): A model for tropospheric calibration from daily surface
and radiosonde balloon measurements, Tech. Memo. 391-350, Jet Propul.
Lab., Pasadena, Calif.
Davis, J. L., T. A. Herring, I. I. Shapiro, A. E. E. Rogers, and G. Elgered
(1985): Geodesy by radio interferometry: Effects of atmospheric modeling
errors on estimates of baseline length, Radio Sci., 20, 1593-1607.
Hogg, D. C., F. O. Guiraud, J. B. Snider, M. T. Decker, and E. R. Westwater
(1983): A steerable dual-channel microwave radiometer for measurement of
water vapor and liquid in the troposphere, J. Clim. Appl. Meteor., 22,
789-806.
Herring, T. A., J. L. Davis, and I. I. Shapiro (1990): Geodesy by radio
interferometry: The application of Kalman filtering to the analysis of very
long baseline interferometry data, J. Geophys. Res., 95, 12561-12581.
Ichikawa, R., M. Kasahara, N. Mannoji, and I. Naito (1994a): An evaluation
of positioning error for space geodetic technique due to azimuthal
asymmetry of wet troposphere delay based on JMA 10 km spectral model data,
Proceedings of The Eighth International Symposium on Recent Crustal
Movements (CRCM '93), pp. 181-187.
Japan Meteorological Agency (1993): Outline of operational numerical
weather prediction at Japan Meteorological Agency, Appendix to Progress
Report on Numerical Prediction Division.
Japan Meteorological Agency (1995): https://www.goin.nasda.go.jp/GOIN/JMA/htdocs/NPD/goin_npd.html
Lorenc, A. C. (1981): A global three-dimensional multivariate statistical
interpolation scheme, Mon. Wea. Rev., 109, 701-721.
Saastamoinen, J. (1972): Contributions to the theory of atmospheric
refraction, part 2, Bull. Geodesique, 107, 13-34, 1972.
Tralli, D. M., S. M. Lichten, and T. A. Herring (1992): Comparison of
Kalman filter estimates of zenith atmospheric path delays using the global
positioning system and very long baseline interferometry, Radio Sci., 27,
999-1007.
Updated on November 2, 1995.
Return to CONTENTS




