Example codes

To use our library, please include the header: #include <lattice/pbkz.hpp>.

Data structure for integer lattices

Our library manipulates integer lattice bases by the type LatticeBasis<T> where T is the type to represent
the Gram-Schmidt coefficients. LatticeBasis has the member "mat_ZZ L" to represent the lattice basis.

For your matrix L of mat_ZZ type, you can subsitute it as:


	mat_ZZ L;
	int dim=50;
        L.SetDims(dim,dim);

	/* Set an example q-ary lattice */
	for (int i=0;i<dim;i++) {
		for (int j=0;j<dim;j++) {
			if (i==j) {
				if (i<dim/2) L[i][j] = dim;
				if (i>=dim/2) L[i][j] = 1;
			} 
			if ((i>=dim/2) && (j<dim/2)) L[i][j] = rand()%dim;
		}
	}
	LatticeBasis<double> B;
	B = L;	//Subsisute your basis
	cout << B << endl; //Display your basis

Example of output is here.

Gram-Schmidt orthogonalizations

After substitution, you can compute Gram-Schmidt coefficients of your basis by:


	B.updateGSBasis();    //compute Gram-Schmidt
	B.gs.displaymu();    //print mu_{i,j}

Example of output is here. Note that the diagonal elements are |b^*_i|².

LLL basis reduction

To find an LLL reduced basis, you cal call


	/*U contains the unimodular matrix corresponding to basis transformation */
	mat_ZZ U;
        U.SetDims(dim,dim);
        for (int i=0;i<dim;i++) U[i][i]=1;	//Initialized by the identity matrix
	double delta=0.99;	//Reduction parameter
	local_LLL(B,&U,delta);
	cout << "B=" << B << endl;	//Display reduced basis
	cout << "U=" << U << endl;	//Display transformation matrix

Example of output.

Generate (Ideal) SVP Challenge instances

If you want to generate several challenge instances, you can do the following.


	//Gram-Schmidt coefficients are computed in long double precision
	LatticeBasis<long double> lB;	
	int dim=100;	//Dimension of challenge instance
	int seed=0;	//Seed of challenge instance
	lB =  svpc::getbasis(dim,seed);	//Call the generator
	BigLLL(lB.L,0,0.999,VL1);	//Call LLL subroutine having huge elements
	cout << lB << endl;	//Display the LLL reduced basis

Example of output.

Note that we call BigLLL() instead of local_LLL because SVP challenge instances are given by Hermite normal forms and they have huge elements.

You can use the function that computes the LLL basis directly:


	lB = svpc::getlllbasis(dim,seed);

Also, to generate instances of Ideal Lattice Challenge, you can call the generator as


	vec_ZZ phi;	//Array to contain the cyclotomic polynomial
	int index = 172;	//Index of challenge instance
	int seed=0;
	lB = isvpc::getlllbasis(index,seed,phi);
	cout << "Lattice Dimension: " << lB.dim << endl;

Progressive BKZ reduction

If you want a reduced basis stronger than LLL, you can use the progressive BKZ subroutine. For the basis above, call the subroutine as


	int beta=60;	//Target BKZ level
	int vl=VL1;	//Display small amount of information
	std::string stringoption="";	//No specific options
	lB.updateGSBasis();    //Before output, need to update GS basis
	lB.gs.gslentofile("gs_lll.txt");    //Output Gram-Schmidt lengths to file
	ProgressiveBKZ<long double>(lB,U,beta,vl,stringoption);
	lB.gs.gslentofile("gs_bkz.txt");    //Output Gram-Schmidt lengths to file

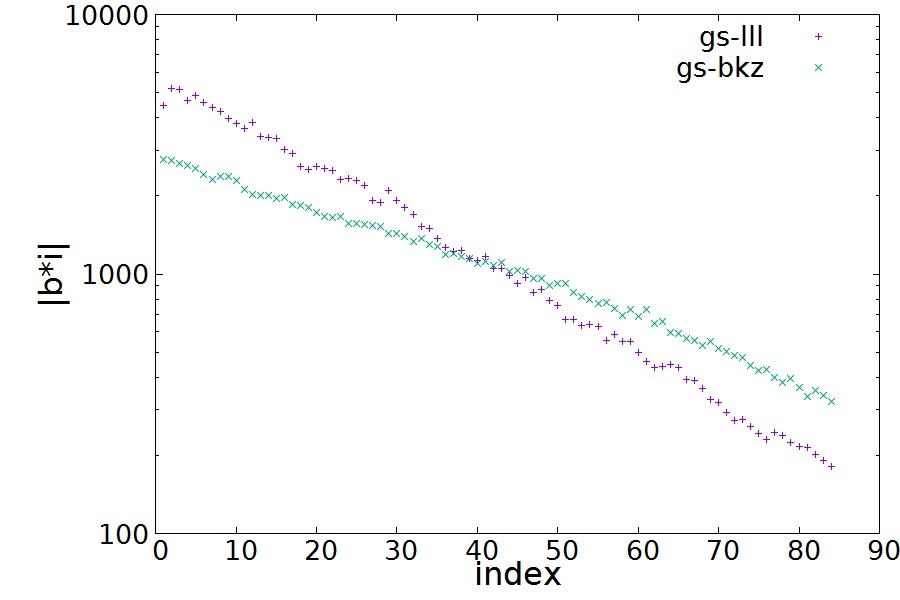
It outputs gs_lll.txt and gs_bkz.txt which have |b^*_i| and |b^*_i|² in the second and third columns, respectively.

Plotting the outputs, you can compare the Gram-Schmidt lengths of reduced basis as follows.

GSlengths